Can you solve this tidal problem?
Tidal Exercise
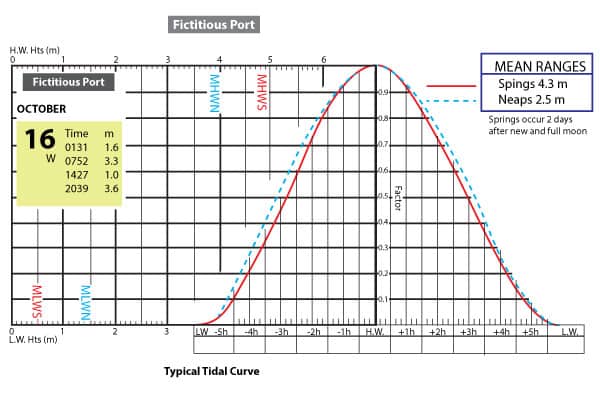
On Wednesday October 16th you are going to sail past this port in the morning. There is a shallow area you’d like to pass over. The tidal information you have obtained is as such.

The chart says the depth of the water of the shallow area is 1 meter. You draw one and a half meters and you would like 1 meter below the keel for safety. Summer daylight savings is in effect.
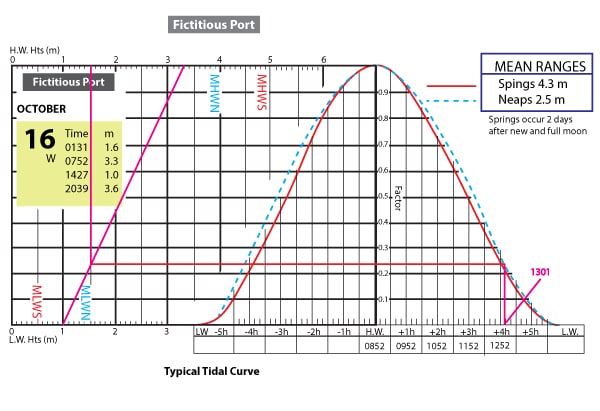
The Tidal Curve for this port is as follows: (click image for downloadable PDF)
Between what times in the morning can you safely pass over the area?
ANSWER:
If you’re just reading this for the first time – think about the question and try to answer it before cheating and dropping straight to the answer.
>>>>>>>>>>
Sorry about this but it was sort of a trick question to get you thinking. Many who emailed us before the deadline of Jan 31st 2015 to win $10 credit towards a NauticEd class got it right – congrats.
Next – apologies for a little ambiguity – the problem did not list if the tide height took into account daylight savings in the tide height listings. Normally they don’t but sometimes they do so Kudos to those who accounted for/discussed this in their answer. We developed the problem using tide heights of NOT using daylight savings – and thus 0131 is 0231, 0752 is 0852, 1427 is 1527 and 2039 is 2139. Actually it doesn’t matter in the answer really because we were only discussing the morning.
To solve: (don’t cheat if you have not answered yet)
First off you need the water to be 2.5 meters deep. 1.5 meters in draft and 1 meter for safety.
Next you need to realize that the reported tide height numbers in a tide table are always listed as the height above the MLLW (mean low low water) datum. So at 0231 the height of the low tide water was 1.6 m above the MLLW datum.
Next realize that chart depths are always listed as the depth of the water at the MLLW datum.
So tide heights and chart depth numbers use the same datum.
Note: USA uses MLLW while most other places use LAT (lowest Attainable Tide). Regardless both are using the same datum in this problem.
This means that at 0231 (low tide) the height of the water in the shallow area was 2.6 m (1 meter depth plus 1.6 meters tide). This is already deeper than the required depth of 2.5 m.
So since 0231 is low tide and the problem asked in the morning then for any time midnight to 0231 the water height is higher than this (0231 is low tide).
Next take a look at the next low tide of 1527 (1427) which is 1 meter. This would not fit the 2.5 meter depth requirement as the depth of the water in the shallow area would be only 1m tide plus 1 meter depth = 2.0 meters. But again the question was “in the morning”. So the question is would there be a time prior to noon where the tide height is lower than 1.5 m?
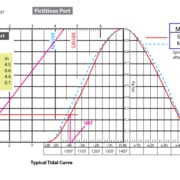
See below for the plot or the ebbing tide. The tide drops from 3.3 meters to 1.0 meters. And the curve to use is neaps since the difference between high and low is 2.3 meters (close to the mean range for neaps at 2.5m) (neaps are when the tide range is less due to the sun and moon not combining their effects – spring is when the sun and moon combine their effects to make the tides higher).
Draw a sloped line on the chart from 3.3 meters to 1 meter. Now drop a line down from 1.5 meters to the sloped line. Bring this intersection point across to the neaps tide curve for the descending tide. Add in the times starting with 0852 being the high tide and adding 1 hour per section. When you hit the neaps curve drop down to the time. The time shows 1301 (each tick is 10 minutes). Thus at 1301 the tide height will be 1.5 meters which is the threshold. Thus you’d have to be clear of the shallow area before 1301.
Since the question asked for the morning – the answer is anytime in the morning. If you made the assumption that the tide height time did include daylight savings then your answer would have been 1201 which still meets the question answer for anytime in the morning.
ANSWER – ANYTIME IN THE MORNING!
Answer to the tide curve problem is anytime in the morning.
Understanding tides is essential.
Common mistakes made in the sent in answers to this question were:
- Using the rule of twelves (no the tide curve was provided)
- Not knowing how to use a tide curve
- Assuming linear dropping of the tide
- Not realizing that the same datum for tides and chart depth are the same.
- Not reading the problem properly
- And pure not understanding the concept of tides e.g. neaps, springs, sinusoidal type rise and fall
Here is a great Comment regarding extra practical thoughts around this problem given to us by Michael Sisley Instructor and free lance yacht skipper. Thanks Michael!
Our sport is fun when we plan in order to make it safe!
1)Read the question. – in a harbour right? Flat water. 1m clearance to allow for uncalculated variables such as atmospheric pressure, on shore wind, shifting sands – good seamanship built into the plan. Yes 2m waves on the sandbar leading to the harbour entrance, an ebbing tide and a strong on shore wind would lead to a very different contingency.
It’s all a matter of preparation and planning.
2) Before setting out, check the your depth echo sounder with a lead line.
3) Harbours silt up and sand bars shift with the tide. So contact the harbour master and ask “Where is the shallow patch now?” “How deep?”
4) The hydrographical service publishes valuable information – use it! You can then use your calculation to help decide when it is safe to go. – And enjoy!
If you learned something in this exercise, perhaps you should take our NauticEd Coastal Navigation Course or take the NauticEd RYA Day Skipper Course and earn your ICC.
Huge congrats to those who solved the problem using the tide curve plot.
If you liked this problem – make sure you friend us on facebook – we will announce there when we post a new one.
Here is the next tide problem.
Read our blog on the Rule of Twelves for tides