Why a Sailboat does not tip over?

Here’s an animation that shows the balance of forces actually it is technically the balance of moments. First off then we’d better explain moments. Simply explained, If you hold your hand out straight and some one puts a pound weight in your hand that is harder to hold than if they put the same pound on your elbow. Even easier – if they put the pound weight right by your shoulder. It’s the same pound weight but it was the Moment that was straining your muscles not the weight. Moment then is weight x distance.

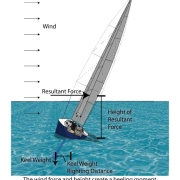
• What tends to tip the boat over is the moment of the wind force high up in the sails.
• What tends to right the boat back  is the keel weight and the distance it is off center.

So now watch the animation 10 times over or so and watch each dynamic as it is happening. Then refer to my extra text below.

Use the green “incr. wind” button. This interactive animation is best observed using Google Chrome browser.

We’ve said it many times over in our courses that the force on the sails is the pressure x the area on the sails on which the wind is acting on. The pressure is proportional to the velocity of the wind squared. Why? – just is.

And from above the Moment is the force x height of the place where the wind is considered to singularly act. This is called the center of the pressure. The center of pressure is the position on the sail whereby if we replaced all the wind all over the sail with an equal force at some position – that would be the position called the center of pressure. On a right triangle sail the point is 1/3 of the way up the mast.

So the tipping moment is proportional to area, height and wind speed squared.

So what really happens is – the wind tips the boat over a bit, this shifts the  keel weight off centerline a bit. The boat will continue to heel over until the tipping moment by the wind is equal to the moment from the keel being off center. At this point the boat will stop heeling over further and the moments are balanced.

Now the wind picks up again – and again the boat heels over further and the keel does some righting – but also notice that the area of the sail presented to the wind has reduced and also the height to the COP has also reduced. So as the boat heels – area and height decrease on the tipping side of the equation.

At all times for the boat to not continue to heel further the moments of tipping and righting have to be balanced.

i.e. keel weight x distance = area x height x vel²

The only dynamic input to the system is the wind – everything else in the equations are just working to balance the vel²

And notice that all of area, height and keel distance off center are just an output from heel. So it is the heel that is purely balancing the wind force on the rig. Durh we knew that but perhaps you had not seen the equations like this.

Now go back and run the animation some more. Notice that the two moments are always in balance.

So also extrapolate – when the boat heels way way (way) over – there is almost no sail area presented to the wind and the height (h) has reduced also – where as additionally the keel distance off center has moved way out which is acting to pull the keel down (boat upright) again.

So next time you’re out there and the boat heels way (way) over – don’t worry every little thing is going to be alright. You’ve got mathematical equations working in your favor. Area and height are reducing and keel distance off center are increasing.

Best you check the keel bolts every now and again however! Yup that’s be a problem!

Enjoy!

If you liked this – you should take the NauticEd Day Skipper Course. It’s a beginner to intermediate sailing course that gets you quickly up to speed on stuff like this using multimedia teaching. Watch this video and learn about the Skipper Sailing Course.